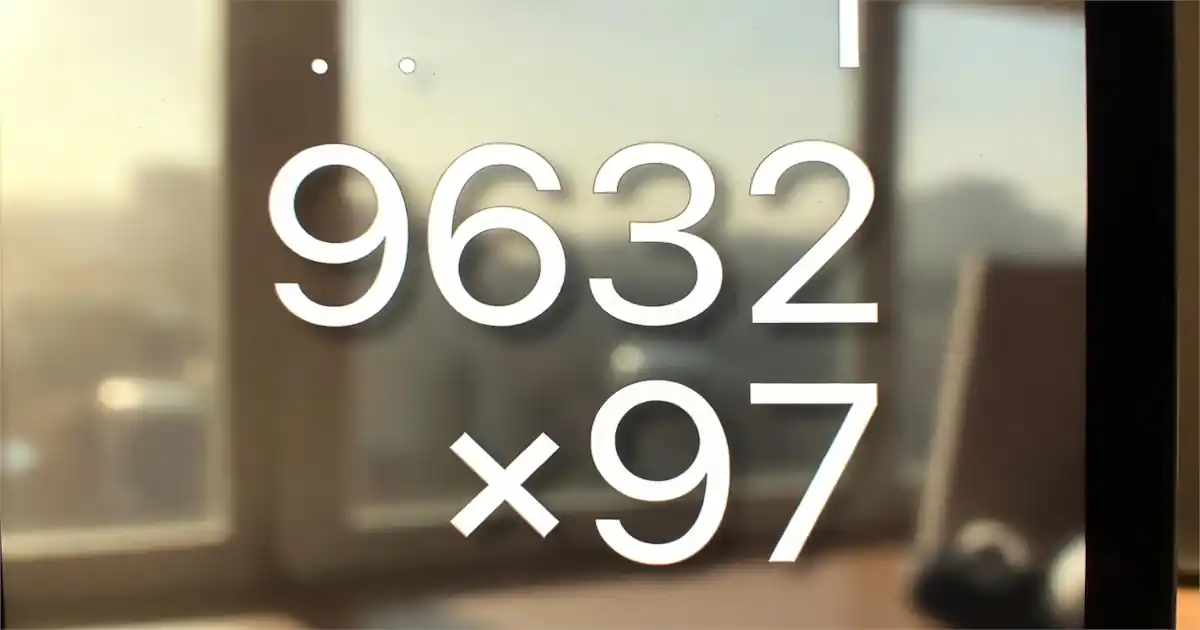
https://techwirepro.com/
Mathematics surrounds us in everyday life. Simple problems can teach us powerful skills. One great example is the multiplication problem 9632×97. Many students and adults struggle with large number multiplication. But with the right method, anyone can solve it quickly. This guide breaks everything down in simple, clear steps. You will understand how to solve it and why the method works.
We will also explore the best strategies to check your answer. By the end, you will feel confident solving similar problems. Let us get started.
What Is 9632×97 and Why Does It Matter?
At first glance, 9632×97 looks like a tricky problem. It involves a four-digit number multiplied by a two-digit number. These types of problems appear often in school, finance, and daily planning. Knowing how to solve them builds your number sense and mental sharpness.
Multiplication is one of the four basic math operations. It helps us calculate quantities quickly. For example, you might need to calculate costs, distances, or areas. A strong grasp of multiplication prepares you for more complex math.
Many people feel anxious about large numbers. But the process is easier than it looks. You only need to follow a clear method step by step. Practice makes these problems feel natural over time.
ALSO READ: How to Download Shotscribus Software for Computer: A Complete Guide
Understanding the Numbers: 9632 and 97
Before we solve any problem, we should understand the numbers involved. The number 9632 is a four-digit number. It sits between 9000 and 10000. Breaking it down: 9000 + 600 + 30 + 2.
The number 97 is very close to 100. This fact is very useful. It means we can use a shortcut method to solve the problem faster. Knowing this saves time and reduces errors.
Understanding your numbers before calculating is a smart habit. Expert mathematicians always analyze the numbers first. This helps them pick the fastest and most accurate method to solve the problem.
Method 1: Standard Long Multiplication
Long multiplication is the traditional method taught in schools. It works for any two numbers, no matter how large. Let us apply it to this problem step by step.
Step 1: Multiply by the Units Digit (7)
First, multiply 9632 by 7. Start from the rightmost digit and work left. 2 x 7 = 14, write 4, carry 1. 3 x 7 = 21, add 1 = 22, write 2, carry 2. 6 x 7 = 42, add 2 = 44, write 4, carry 4. 9 x 7 = 63, add 4 = 67, write 67. Result: 67,424.
Step 2: Multiply by the Tens Digit (9)
Next, multiply 9632 by 9. Remember to shift one place to the left. 2 x 9 = 18, write 8, carry 1. 3 x 9 = 27, add 1 = 28, write 8, carry 2. 6 x 9 = 54, add 2 = 56, write 6, carry 5. 9 x 9 = 81, add 5 = 86, write 86. Result: 86,688 (shifted left = 866,880).
Step 3: Add the Two Results
Now add 67,424 and 866,880 together. The final answer is 934,304. This is the correct solution to the problem. Always double-check your addition at this final step.
Method 2: The Shortcut Trick Using 100
Here is a faster way to solve this problem. Since 97 is close to 100, we can use a clever shortcut. This method is popular in mental math competitions. It saves a lot of time once you understand it.
The idea is simple: 97 = 100 – 3. So instead of multiplying directly, we rewrite the problem. We calculate 9632 x 100, then subtract 9632 x 3. This turns a hard problem into two easier ones.
Step 1: Multiply 9632 by 100 = 963,200. Step 2: Multiply 9632 by 3 = 28,896. Step 3: Subtract: 963,200 – 28,896 = 934,304. The answer matches our earlier result perfectly.
This shortcut works because of the distributive property of multiplication. Breaking numbers into friendly chunks makes calculations faster. Professional accountants and engineers use similar tricks every day.
ALSO READ: When Was the Game Innerlifthunt Released? The Truth Revealed
How to Verify Your Answer
Checking your work is just as important as solving the problem. A small error can lead to a wrong answer. Here are two easy ways to verify your result.
Use Estimation First
Round 9632 to 9600 and 97 to 100. Estimate: 9600 x 100 = 960,000. Our answer of 934,304 is close to this estimate. This confirms we are in the right range.
Reverse Check with Division
Divide your answer by one of the original numbers. 934,304 ÷ 97 should give you 9,632. If the division works out correctly, your multiplication is right. This reverse check is reliable and builds confidence in your answer.
Common Mistakes People Make
Even careful students make mistakes in multiplication. Knowing the common errors helps you avoid them. Here are the most frequent problems people run into.
Forgetting to carry numbers is a very common mistake. When a product exceeds 9, you must carry the tens digit. Missing one carry throws off the entire calculation.
Not shifting the second row is another frequent error. When you multiply by the tens digit, you must add a zero at the end. Skipping this step will give a wrong final total.
Adding the partial products incorrectly is also common. Take your time with the final addition step. Use column alignment carefully. A misaligned column can completely change your result.
Real-World Applications of This Type of Multiplication
You might wonder where this type of math is used in real life. The answer is: almost everywhere. Let us look at a few practical examples that show why this skill matters.
Imagine a factory that produces 9,632 items per day. If they run for 97 days, they produce 934,304 items total. Managers use this kind of math to plan production schedules.
A contractor building homes needs to calculate materials. If each home needs 9,632 bricks and they build 97 homes, they need 934,304 bricks total. Getting this wrong wastes money and time.
Even in personal finance, this skill helps. Multiply a monthly expense by months to plan a budget. These calculations save people from financial surprises. Strong multiplication skills directly support better life decisions.
Tips to Get Better at Large Number Multiplication
Getting better at multiplication takes consistent practice. You do not need to be naturally gifted at math. Anyone can improve with the right habits and tools.
Practice your times tables every day. Strong basic multiplication facts speed up every calculation. Even 10 minutes a day leads to significant improvement over weeks.
Use grid paper or lined paper to keep your columns aligned. Misaligned digits cause errors in multi-digit multiplication. Neat work leads to accurate results.
Learn shortcut methods like the one we used for 9632×97. These techniques help you solve problems faster during tests and in everyday situations. Practice each shortcut until it feels natural.
Always estimate before solving and check after. This habit catches errors early. Experienced mathematicians and engineers always verify their work. You should too.
Tools That Can Help You Solve and Check Problems
While learning by hand is important, tools can support your practice. Calculators are great for checking your work after solving it manually. Do not use them as a shortcut before trying yourself.
Online math tools and apps can also help you practice multiplication. Many free websites offer step-by-step solutions. Use them to understand where you went wrong, not just to get the answer.
Flashcard apps are excellent for building times table fluency. Strong mental math foundations make large problems like this much easier. Invest time in the basics and the harder problems become simple.
Conclusion: Mastering Multiplication Step by Step
The problem 9632×97 is a great example of how structured thinking solves big challenges. We explored two solid methods: long multiplication and the shortcut trick. Both give the same correct answer: 934,304.
We also covered how to verify your answer and avoid common mistakes. Real-world examples showed how this type of math applies in daily life. And we shared practical tips to keep improving your skills.
Math is not about being born smart. It is about learning the right approach and practicing consistently. Every expert was once a beginner who kept trying.
Start with one method, master it, then try the shortcut. Use estimation to check your range. Use division to verify your answer. With these habits, you will handle any large multiplication problem with confidence.